Логарифмические неравенства — Гипермаркет знаний. Решение простейших логарифмических неравенств

До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.

Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.

1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи « » и « ».

2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.

3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».

Пересечением множеств называется множество, которому принадлежат только те элементы, которые есть у каждого из этих множеств.

пересечением

Изображение пересечения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. У Дианы в сумочке находится «множество», состоящее из {ручки , карандаша , линейки , тетрадки , расчески }. У Алисы в сумочке находится «множество», состоящее из {записной книжки , карандаша , зеркальца , тетрадки , котлеты по-киевски }. Пересечением этих двух «множеств» будет «множество», состоящее из {карандаша , тетрадки }, поскольку оба этих «элемента» есть и у Дианы, и у Алисы.

Важно запомнить! Если решением неравенства является промежуток а решением неравенства является промежуток то решением систем:

является промежуток то есть пересечение исходных промежутков. Здесь и далее под подразумевается любой из знаков title="Rendered by QuickLaTeX.com" height="17" width="93" style="vertical-align: -4px;">а под — ему противоположный знак.

Объединением множеств называется множество, которое состоит из всех элементов исходных множеств.

Другими словами, если даны два множества и то их объединением будет являться множество следующего вида:

Изображение объединения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из {ручки , карандаша , линейки , тетрадки , расчески , записной книжки , зеркальца , котлеты по-киевски }, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может содержать в себе одинаковых элементов.

Важно запомнить! Если решением неравенства является промежуток а решением неравенства является промежуток то решением совокупности:

является промежуток то есть объединение исходных промежутков.

Перейдем непосредственно к примерам.

Пример 1. Решите систему неравенств:

Решение задачи C3.

1. Решаем сперва первое неравенств. Используя замену переходим к неравенству:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется неравенством:

Title="Rendered by QuickLaTeX.com">

В области допустимых значений с учетом того, что основание логарифма title="Rendered by QuickLaTeX.com" height="18" width="52" style="vertical-align: -4px;"> переходим к равносильному неравенству:

Исключая решения, не входящие в область допустимых значений, получаем промежуток

3. Ответом к системе неравенств будет пересечение

Полученные промежутки на числовой прямой. Решение — их пересечение

Пример 2. Решите систему неравенств:

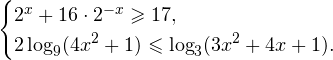
Решение задачи C3.

1. Решаем сперва первое неравенство. Умножаем обе части на title="Rendered by QuickLaTeX.com" height="14" width="55" style="vertical-align: 0px;"> и делаем замену в результате чего приходим к неравенству:

Переходим к обратной подстановке:

2.

Title="Rendered by QuickLaTeX.com">

Графическое изображение полученных промежуток. Решение системы — их пересечение

Пример 3. Решите систему неравенств:

Решение задачи C3.

1. Решаем сперва первое неравенство. Умножаем обе его части на title="Rendered by QuickLaTeX.com" height="18" width="61" style="vertical-align: -4px;"> после чего получаем неравенство:

Используя подстановку переходим к следующему неравенству:

Переходим к обратной подстановке:

2. Решаем теперь второе неравенство. Определим сначала область допустимых значений этого неравенства:

ql-right-eqno">

Обращаем внимание, что

Тогда с учетом области допустимых значений получаем:

3. Находим общее решения неравенств. Сравнение полученных иррациональных значений узловых точек — задача в данном примере отнюдь не тривиальная. Сделать это можно следующим образом. Так как

Title="Rendered by QuickLaTeX.com">

то и окончательный ответ к системе имеет вид:

Пример 4. Решите систему неравенств:

Решение задачи С3.

1. Решим сперва второе неравенство:

2. Первое неравенство исходной системы представляет собой логарифмическое неравенство с переменным основанием. Удобный способ решения подобных неравенств описан в статье «Сложные логарифмические неравенства », в его основе лежит простая формула:

Вместо знака может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства:

Определим теперь область допустимых значений данного неравенства. Она задается следующей системой:

Title="Rendered by QuickLaTeX.com">

Title="Rendered by QuickLaTeX.com">

Легко видеть, что одновременно этот промежуток будет являться и решением нашего неравенства.

3. Окончательным ответом исходной системы неравенств будет пересечение полученных промежутков, то есть

Пример 5. Решите систему неравенств:

Решение задания C3.

1. Решаем сперва первое неравенство. Используем подстановку Переходим к следующему квадратному неравенству:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

Title="Rendered by QuickLaTeX.com">

Данное неравенство равносильно следующей смешанной системе:

В области допустимых значений, то есть при title="Rendered by QuickLaTeX.com" height="18" width="53" style="vertical-align: -4px;"> используя равносильные преобразования переходим к следующей смешанной системе:

С учетом области допустимых значений получаем:

3. Окончательным решением исходной системы является

Решение задачи C3.

1. Решаем сперва первое неравенство. Равносильными преобразованиями приводим его к виду:

2. Решаем теперь второе неравенство. Область его допустимых значений определяется промежутком: title="Rendered by QuickLaTeX.com" height="14" width="68" style="vertical-align: 0px;"> Используя замену переменной переходим к следующему квадратичному неравенству:

Этот ответ целиком принадлежит области допустимых значений неравенства.

3. Пересечением полученных в предыдущих пунктах промежутков получаем окончательный ответ к системе неравенств:

Сегодня мы с вами решали системы логарифмических и показательных неравенств. Задания подобного рода предлагались в пробных вариантах ЕГЭ по математике в течение всего ныне идущего учебного года. Однако, как репетитор по математике, имеющий опыт подготовки к ЕГЭ, могу сказать, что это вовсе не означает, что аналогичные задания будут в реальных вариантах ЕГЭ по математике в июне.

Позволю себе высказать одно предостережение, адресованное в первую очередь репетиторам и школьным учителям, занимающимся подготовкой старшеклассников к сдаче ЕГЭ по математике. Весьма опасно готовить школьников к экзамену строго по заданным темам, ведь в этом случае возникает риск полностью «завалить» его даже при незначительном изменении ранее заявленного формата заданий. Математическое образование должно быть полным. Уважаемые коллеги, пожалуйста, не уподобляйте роботам своих учеников так называемым «натаскиванием» на решение определенного типа задач. Ведь нет ничего хуже формализации мышления человека.

Всем удачи и творческих успехов!

Сергей Валерьевич

Если пробовать, то есть два варианта: получится или не получится. Если не пробовать — всего один.
© Народная мудрость

Цели урока:

Дидактические:

• 1 уровень – научить решать простейшие логарифмические неравенства, применяя определение логарифма, свойства логарифмов;
• 2 уровень – решать логарифмические неравенства, выбирая самостоятельно способ решения;
• 3 уровень – уметь применять знания и умения в нестандартных ситуациях.

Развивающие: развивать память, внимание, логическое мышление, навыки сравнения, уметь обобщать и делать выводы

Воспитательные: воспитывать аккуратность, ответственность за выполняемое задание, взаимопомощь.

Методы обучения: словесный, наглядный, практический, частично-поисковый, самоуправления, контроля.

Формы организации познавательной деятельности учащихся: фронтальный, индивидуальный, работа в парах.

Оборудование: набор тестовых заданий, опорный конспект, чистые листы для решений.

Тип урока: изучение нового материала.

Ход урока

1. Организационный момент. Объявляются тема и цели урока, схема проведения урока: каждому ученику выдается оценочный лист, который ученик заполняет в течении урока; для каждой пары учеников – печатные материалы с заданиями, выполнять задания нужно в парах; чистые листы для решений; опорные листы: определение логарифма; график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств.

Все решения после самооценки сдаются учителю.

Оценочный лист учащегося

2. Актуализация знаний.

Указания учителя. Вспомните определение логарифма, график логарифмической функции и ее свойства. Для этого прочитайте текст на с.88–90, 98–101 учебника “Алгебра и начала анализа 10–11” под редакцией Ш.А Алимова, Ю.М Колягина и др.

Ученикам раздаются листы, на которых записаны: определение логарифма; изображен график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств, пример решения логарифмического неравенства, сводящегося к квадратному.

3. Изучение нового материала.

Решение логарифмических неравенств основано на монотонности логарифмической функции.

Алгоритм решения логарифмических неравенств:

А) Найти область определения неравенства (подлогарифмическое выражение больше нуля).
Б) Представить (если возможно) левую и правую части неравенства в виде логарифмов по одному и тому же основанию.
В) Определить, возрастающей или убывающей является логарифмическая функция: если t>1, то возрастающая; если 01, то убывающая.
Г) Перейти к более простому неравенству (подлогарифмических выражений), учитывая, что знак неравенства сохранится, если функция возрастает, и изменится, если она убывает.

Учебный элемент № 1.

Цель: закрепить решение простейших логарифмических неравенств

Форма организации познавательной деятельности учащихся: индивидуальная работа.

Задания для самостоятельной работы на 10 минут. Для каждого неравенства имеются несколько вариантов ответов, нужно выбрать верный и проверить по ключу.

КЛЮЧ: 13321, максимальное кол-во баллов – 6 б.

Учебный элемент № 2.

Цель: закрепить решение логарифмических неравенств, применяя свойства логарифмов.

Указания учителя. Вспомните основные свойства логарифмов. Для этого прочитайте текст учебника на с.92, 103–104.

Задания для самостоятельной работы на 10 минут.

КЛЮЧ: 2113, максимальное кол-во баллов – 8 б.

Учебный элемент № 3.

Цель: изучить решение логарифмических неравенств методом сведения к квадратному.

Указания учителя: метод сведения неравенства к квадратному состоит в том, что нужно преобразовать неравенство к такому виду, чтобы некоторую логарифмическую функцию обозначить новой переменной, получив при этом квадратное неравенство относительно этой переменной.

Применим метод интервалов.

Вы прошли первый уровень усвоения материала. Теперь вам придется самостоятельно выбрать метод решения логарифмических уравнений, используя все свои знания и возможности.

Учебный элемент № 4.

Цель: закрепить решение логарифмических неравенств, выбрав самостоятельно рациональный способ решения.

Задания для самостоятельной работы на 10 минут

Учебный элемент № 5.

Указания учителя. Молодцы! Вы освоили решение уравнений второго уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных и нестандартных ситуациях.

Задания для самостоятельного решения:

Указания учителя. Замечательно, если вы справились со всем заданием. Молодцы!

Оценка за весь урок зависит от числа набранных баллов по всем учебным элементам:

• если N ≥ 20, то вы получаете оценку “5”,
• при 16 ≤ N ≤ 19 – оценка “4”,
• при 8 ≤ N ≤ 15 – оценка “3”,
• при N < 8 выполнить работу над ошибками к следующему уроку (решения можно взять у учителя).

Оценочные лисы сдать учителю.

5. Домашнее задание: если вы набрали не более 15 б – выполните работу над ошибками (решения можно взять у учителя), если вы набрали более 15 б – выполните творческое задание по теме “Логарифмические неравенства”.

Вам кажется, что до ЕГЭ еще есть время, и вы успеете подготовиться? Быть может, это и так. Но в любом случае, чем раньше школьник начинает подготовку, тем успешнее он сдает экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одно из заданий, а значит, возможность получить дополнительный балл.

Вы уже знаете, что такое логарифм(log)? Мы очень надеемся, что да. Но даже если у вас нет ответа на этот вопрос, это не проблема. Понять, что такое логарифм очень просто.

Почему именно 4? В такую степень нужно возвести число 3, чтобы получилось 81. Когда вы поняли принцип, можно приступать и к более сложным вычислениям.

Неравенства вы проходили еще несколько лет назад. И с тех пор они постоянно встречаются вам в математике. Если у вас проблемы с решением неравенств, ознакомьтесь с соответствующим разделом.
Теперь, когда мы познакомились с понятиями по отдельности, перейдем к их рассмотрению в общем.

Самое простое логарифмическое неравенство.

Простейшие логарифмические неравенства не ограничиваются этим примером, есть еще три, только с другими знаками. Зачем это нужно? Чтобы полнее понять, как решать неравенство с логарифмами. Теперь приведем более применимый пример, все еще достаточно простой, сложные логарифмические неравенства оставим на потом.

Как это решить? Все начинается с ОДЗ. О нем стоит знать больше, если хочется всегда легко решать любое неравенство.

Что такое ОДЗ? ОДЗ для логарифмических неравенств

Аббревиатура расшифровывается как область допустимых значений. В заданиях для ЕГЭ нередко всплывает данная формулировка. ОДЗ пригодится вам не только в случае логарифмических неравенств.

Посмотрите еще раз на вышеприведенный пример. Мы будем рассматривать ОДЗ, исходя из него, чтобы вы поняли принцип, и решение логарифмических неравенств не вызывало вопросов. Из определения логарифма следует что, 2х+4 должно быть больше нуля. В нашем случае это означает следующее.

Это число по определению должно быть положительным. Решите неравенство, представленное выше. Это можно сделать даже устно, здесь явно, что X не может быть меньше 2. Решение неравенства и будет определением области допустимых значений.
Теперь перейдем к решению простейшего логарифмического неравенства.

Отбрасываем из обеих частей неравенства сами логарифмы. Что в результате у нас остается? Простое неравенство.

Решить его несложно. X должен быть больше -0,5. Теперь совмещаем два полученных значения в систему. Таким образом,

Это и будет область допустимых значений для рассматриваемого логарифмического неравенства.

Зачем вообще нужно ОДЗ? Это возможность отсеять неверные и невозможные ответы. Если ответ не входит в область допустимых значений, значит, ответ попросту не имеет смысла. Это стоит запомнить надолго, так как в ЕГЭ часто встречается необходимость поиска ОДЗ, и касается она не только логарифмических неравенств.

Алгоритм решения логарифмического неравенства

Решение состоит из нескольких этапов. Во-первых, необходимо найти область допустимых значений. В ОДЗ будет два значения, это мы рассмотрели выше. Далее нужно решить само неравенство. Методы решения бывают следующими:

• метод замены множителей;
• декомпозиции;
• метод рационализации.

В зависимости от ситуации стоит применять один из вышеперечисленных методов. Перейдем непосредственно к решению. Раскроем наиболее популярный метод, который подходит для решения заданий ЕГЭ практически во всех случаях. Далее мы рассмотрим метод декомпозиции. Он может помочь, если попалось особенно «заковыристое» неравенство. Итак, алгоритм решения логарифмического неравенства.

Примеры решения :

Мы не зря взяли именно такое неравенство! Обратите внимание на основание. Запомните: если оно больше единицы, знак остается прежним при нахождении области допустимых значений; в противном случае нужно изменить знак неравенства.

В результате мы получаем неравенство:

Теперь приводим левую часть к виду уравнения, равному нулю. Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы найдем ОДЗ. Надеемся, что с решением такого простого уравнения у вас не будет проблем. Ответы -4 и -2. Это еще не все. Нужно отобразить эти точки на графике, расставить «+» и «-». Что нужно для этого сделать? Подставить в выражение числа из интервалов. Где значения положительны, там ставим «+».

Ответ : х не может быть больше -4 и меньше -2.

Мы нашли область допустимых значений только для левой части, теперь нужно найти область допустимых значений правой части. Это не в пример легче. Ответ: -2. Пересекаем обе полученные области.

И только теперь начинаем решать само неравенство.

Упростим его, насколько возможно, чтобы решать было легче.

Снова применяем метод интервалов в решении. Опустим выкладки, с ним уже и так все понятно по предыдущему примеру. Ответ.

Но этот метод подходит, если логарифмическое неравенство имеет одинаковые основания.

Решение логарифмических уравнений и неравенств с разными основаниями предполагает изначальное приведение к одному основанию. Далее применяйте вышеописанный метод. Но есть и более сложный случай. Рассмотрим один из самых сложных видов логарифмических неравенств.

Логарифмические неравенства с переменным основанием

Как решать неравенства с такими характеристиками? Да, и такие могут встретиться в ЕГЭ. Решение неравенств нижеследующим способом тоже полезно скажется на вашем образовательном процессе. Разберемся в вопросе подробным образом. Отбросим теорию, перейдем сразу к практике. Чтобы решать логарифмические неравенства, достаточно однажды ознакомиться с примером.

Чтобы решить логарифмическое неравенство представленного вида, необходимо привести правую часть к логарифму с тем же основанием. Принцип напоминает равносильные переходы. В итоге неравенство будет выглядеть следующим образом.

Собственно, остается создать систему неравенств без логарифмов. Используя метод рационализации, переходим к равносильной системе неравенств. Вы поймете и само правило, когда подставите соответствующие значения и проследите их изменения. В системе будут следующие неравенства.

Воспользовавшись методом рационализации при решении неравенств нужно помнить следующее: из основания необходимо вычесть единицу, х по определению логарифма из обеих частей неравенства вычитается (правое из левого), два выражения перемножаются и выставляются под исходным знаком по отношению к нулю.

Дальнейшее решение осуществляется методом интервалов, здесь все просто. Вам важно понять отличия в методах решения, тогда все начнет легко получаться.

В логарифмических неравенствах много нюансов. Простейшие из них решать достаточно легко. Как сделать так, чтобы решать каждое из них без проблем? Все ответы вы уже получили в этой статье. Теперь впереди вас ждет длительная практика. Постоянно практикуйтесь в решении самых разных задач в рамках экзамена и сможете получить наивысший балл. Успехов вам в вашем непростом деле!

Введение

Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития. Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером(1550-1617) и швейцарцем Иобстом Бюрги(1552-1632) Первым опубликовал работу Непер в 1614г. под названием «Описание удивительной таблицы логарифмов», теория логарифмов Непера была дана в достаточно полном объёме, способ вычисления логарифмов дан наиболее простой, поэтому заслуги Непера в изобретении логарифмов больше, чем у Бюрги. Бюрги работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620г. Идеей логарифма Непер овладел около1594г. хотя таблицы опубликовал через 20 лет. Вначале он называл свои логарифмы «искусственными числами» и уже потом предложил эти «искусственные числа» называть одним словом «логарифм», который в переводе с греческого- «соотнесённые числа», взятые одно из арифметической прогресси, а другое из специально подобранной к ней геометрической прогресси. Первые таблицы на русском языке были изданы в1703г. при участии замечательного педагога 18в. Л. Ф Магницкого. В развитии теории логарифмов большое значение имели работы петербургского академика Леонарда Эйлера. Он первым стал рассматривать логарифмирование как действие, обратное возведению в степень, он ввёл в употребление термины «основание логарифма» и «мантисса» Бригс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического употребления, теория их проще, чем у логарифмов Непера. Поэтому десятичные логарифмы иногда называют бригсовыми. Термин «характеристика» ввёл Бригс.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Логарифмические уравнения и неравенства

1. Логарифмические уравнения

Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением.

Простейшим логарифмическим уравнением является уравнение вида

log a x = b . (1)

Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = a b .

Пример 1. Решить уравнения:

a) log 2 x = 3, b) log 3 x = -1, c)

Решение. Используя утверждение 1, получим a) x = 2 3 или x = 8; b) x = 3 -1 или x = 1 / 3 ; c)

или x = 1.

Приведем основные свойства логарифма.

Р1. Основное логарифмическое тождество:

где a > 0, a ≠ 1 и b > 0.

Р2. Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:

log a N 1 ·N 2 = log a N 1 + log a N 2 (a > 0, a ≠ 1, N 1 > 0, N 2 > 0).

Замечание. Если N 1 ·N 2 > 0, тогда свойство P2 примет вид

log a N 1 ·N 2 = log a |N 1 | + log a |N 2 | (a > 0, a ≠ 1, N 1 ·N 2 > 0).

Р3. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя

(a > 0, a ≠ 1, N 1 > 0, N 2 > 0).

Замечание. Если

, (что равносильно N 1 N 2 > 0) тогда свойство P3 примет вид (a > 0, a ≠ 1, N 1 N 2 > 0).

P4. Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:

log a N k = k log a N (a > 0, a ≠ 1, N > 0).

Замечание. Если k - четное число (k = 2s ), то

log a N 2s = 2s log a |N | (a > 0, a ≠ 1, N ≠ 0).

P5. Формула перехода к другому основанию:

(a > 0, a ≠ 1, b > 0, b ≠ 1, N > 0),

в частности, если N = b , получим

(a > 0, a ≠ 1, b > 0, b ≠ 1). (2)

Используя свойства P4 и P5, легко получить следующие свойства

(a > 0, a ≠ 1, b > 0, c ≠ 0), (3) (a > 0, a ≠ 1, b > 0, c ≠ 0), (4) (a > 0, a ≠ 1, b > 0, c ≠ 0), (5)

и, если в (5) c - четное число (c = 2n ), имеет место

(b > 0, a ≠ 0, |a | ≠ 1). (6)

Перечислим и основные свойства логарифмической функции f (x ) = log a x :

1. Область определения логарифмической функции есть множество положительных чисел.

2. Область значений логарифмической функции - множество действительных чисел.

3. При a > 1 логарифмическая функция строго возрастает (0 < x 1 < x 2 log a x 1 < log a x 2), а при 0 < a < 1, - строго убывает (0 < x 1 < x 2 log a x 1 > log a x 2).

4. log a 1 = 0 и log a a = 1 (a > 0, a ≠ 1).

5. Если a > 1, то логарифмическая функция отрицательна при x (0;1) и положительна при x (1;+∞), а если 0 < a < 1, то логарифмическая функция положительна при x  (0;1) и отрицательна при x (1;+∞).

6. Если a > 1, то логарифмическая функция выпукла вверх, а если a (0;1) - выпукла вниз.

Следующие утверждения (см., например, ) используются при решении логарифмических уравнений.